• 道路通行能力

道路通行能力

---

引言#

道路的通行能力通常以“辆/小时”表示，描述了道路能够处理的最大交通流量。

根据经验法则，多车道道路的通行能力是单车道通行能力与车道数的乘积。确切的关系更为复杂，取决于车辆速度的分布和换道动力学。

车道通行能力#

单车道的通行能力与连续车辆之间的时间间距成反比。假设交通流均匀且间距相等：

capacity = 3600 / grossTimeHeadway

其中 grossTimeHeadway 表示两辆连续车辆的前保险杠通过同一地点所需的时间。

相比之下，netTimeHeadway 表示跟随车辆的前保险杠到达前车后保险杠位置所需的时间。

间距计算#

仿真中观察到的确切时间间距取决于所使用的车辆跟驰模型（carFollowModel）及其参数。最容易分析的情况是所有车辆以相同的速度 s 行驶。

令 grossHeadway 表示连续车辆前保险杠之间的距离，netHeadway 表示跟随车辆前保险杠到前车后保险杠的距离。

对于默认的 'Krauss' 模型，以下 vType 属性与最小时间间距（对应于最大流量，即车道通行能力）相关：

• length: 车辆的物理长度，单位为米（默认 5）
• minGap: 静止队列中车辆间的最小间距，单位为米（默认 2.5）
• tau: 期望的最小时间间距，单位为秒（默认 1）

假设所有车辆都以恒定速度 s 行驶，'Krauss' 模型的间距关系如下：

• netHeadway = minGap + tau * s
• grossHeadway = length + minGap + tau * s

由此我们可以直接计算出时间间距：

• netTimeHeadway = minGap / s + tau
• grossTimeHeadway = (length + minGap) / s + tau

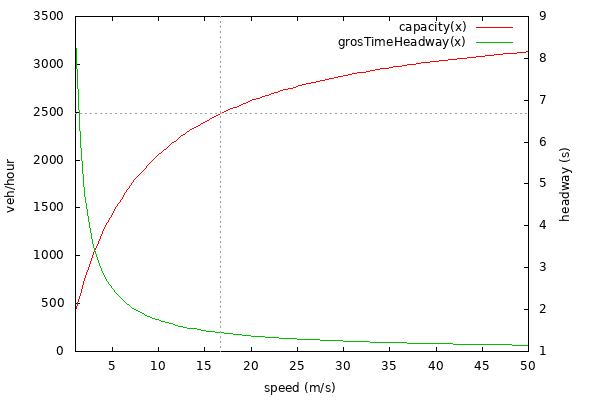
由于长度（length）和最小间距（minGap）的存在，道路的通行能力取决于其限速（而 tau 分量与速度无关）。 在高速行驶时，tau 分量是主导因素，而在低速时，长度和最小间距占主导地位。

下图显示了在默认模型参数（length、minGap 和 tau）下，不同道路速度对应的理想时间间距和道路通行能力。

进一步的间距影响#

上述计算仅适用于车辆以恒定速度行驶且保持最小距离的情况。这在仿真中很少发生，原因如下：

• 车辆有不同的期望速度（建模为 speedFactor 分布）
• 车辆有随机的减速（取决于跟驰模型）。
• 车辆并不总是处于最小跟驰距离的配置中。必须特别注意车辆插入。

下表显示了根据所使用的 vType 和插入参数，在车辆插入时可达到的道路通行能力。道路限速为 16.66m/s，理论通行能力为 2482 辆/小时。生成下表数据点的脚本可以在这里找到。

sigma	speedDev	departSpeed	capacity	capacity --step-length 0.1	capacity --extrapolate-departpos	capacity --step-length 0.1 --extrapolate-departpos
0.5	0.1	0	1198	1368	1198	1368
0.5	0.1	max	1635	2183	1653	2186
0.5	0.1	desired	1522	2052	1921	2090
0.5	0.1	avg	1933	2206	1974	2211
0.5	0	0	1200	1368	1200	1368
0.5	0	max	1643	2188	1664	2188
0.5	0	desired	1800	2400	2128	2441
0.5	0	avg	1800	2400	2142	2446
0	0.1	0	1440	1500	1440	1500
0	0.1	max	2075	2276	2087	2276
0	0.1	desired	1663	2080	2190	2183
0	0.1	avg	2199	2238	2235	2243
0	0	0	1440	1500	1440	1500
0	0	max	2073	2489	2083	2489
0	0	desired	1800	2400	2482	2483
0	0	avg	1800	2400	2482	2483

注释

• 默认的 departSpeed 为 '0'，这导致了最差的插入通行能力
• 默认的 sigma 为 '0.5'，乘用车的默认 speedDev 为 0.1
• 对于默认的 Krauss 模型，步长（step-length）对 sigma 导致的平均速度降低有副作用（可以通过在 vType 中设置 sigmaStep="1" 来补救）

双车道道路上的插入通行能力#

下表显示了在双车道道路上，根据所使用的插入参数，在车辆插入时可达到的道路通行能力。道路限速为 16.66m/s，理论通行能力为 4964 辆/小时。生成下表数据点的脚本可以在这里找到。

• sigma 恒定为 0.5
• speedDev 恒定为 0.1

departLane	departSpeed	capacity	capacity --step-length 0.1	capacity --extrapolate-departpos	capacity --step-length 0.1 --extrapolate-departpos
first	max	1664	3224	1657	3210
random	max	3289	4370	3298	4376
free	max	3279	4378	3304	4379
best_prob	max	3331	4419	3321	4432
first	avg	1922	2653	2385	2763
random	avg	3881	4421	3972	4426
free	avg	3870	4432	3970	4431
best_prob	avg	3878	4500	4039	4512

三车道道路上的插入通行能力#

下表显示了在三车道道路上，根据所使用的插入参数，在车辆插入时可达到的道路通行能力。道路限速为 16.66m/s，理论通行能力为 7447 辆/小时。生成下表数据点的脚本可以在这里找到。

• sigma 恒定为 0.5
• speedDev 恒定为 0.1

departLane	departSpeed	capacity	capacity --step-length 0.1	capacity --extrapolate-departpos	capacity --step-length 0.1 --extrapolate-departpos
first	max	1647	3216	1656	3224
random	max	4952	6569	4953	6575
free	max	4936	6568	4956	6562
best_prob	max	5068	6683	5053	6706
first	avg	1907	2623	2369	2708
random	avg	5826	6626	5958	6639
free	avg	5794	6641	5951	6659
best_prob	avg	5718	6845	6136	6854